Ontario Economic Accounts
Learn about Ontario's economic performance and outlook for the third quarter of 2025.
View the related data tables at Ontario's Open Data Catalogue.
Highlights
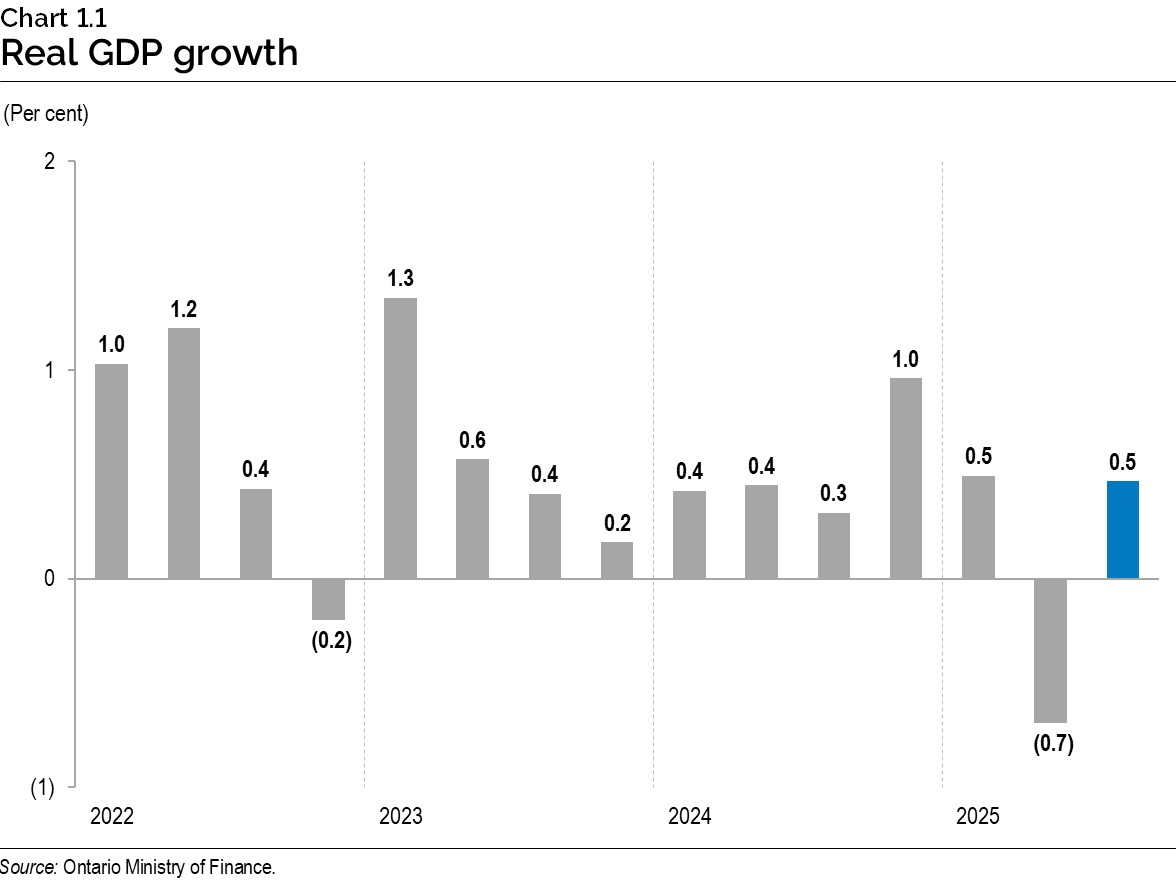
- Ontario’s real gross domestic product (GDP) advanced 0.5% in the third quarter (July, August, September) of 2025, following a 0.7% decline in the previous quarter.
- Third quarter growth was supported by gains in residential investment and net trade as exports edged up and imports declined.
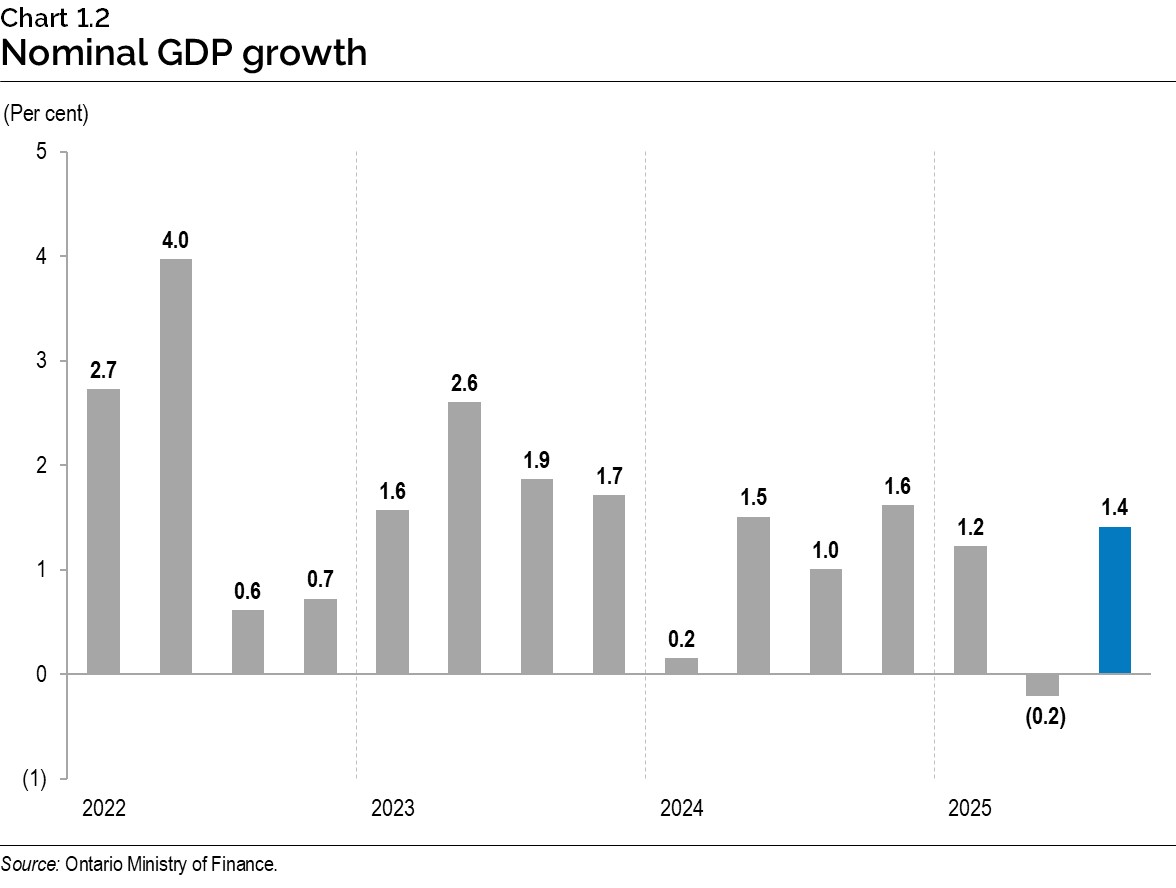
- Nominal GDP rose 1.4%, following a 0.2% decline in the previous quarter.
- Economy-wide prices, as measured by the implicit price index for GDP, increased 0.9% in the third quarter.
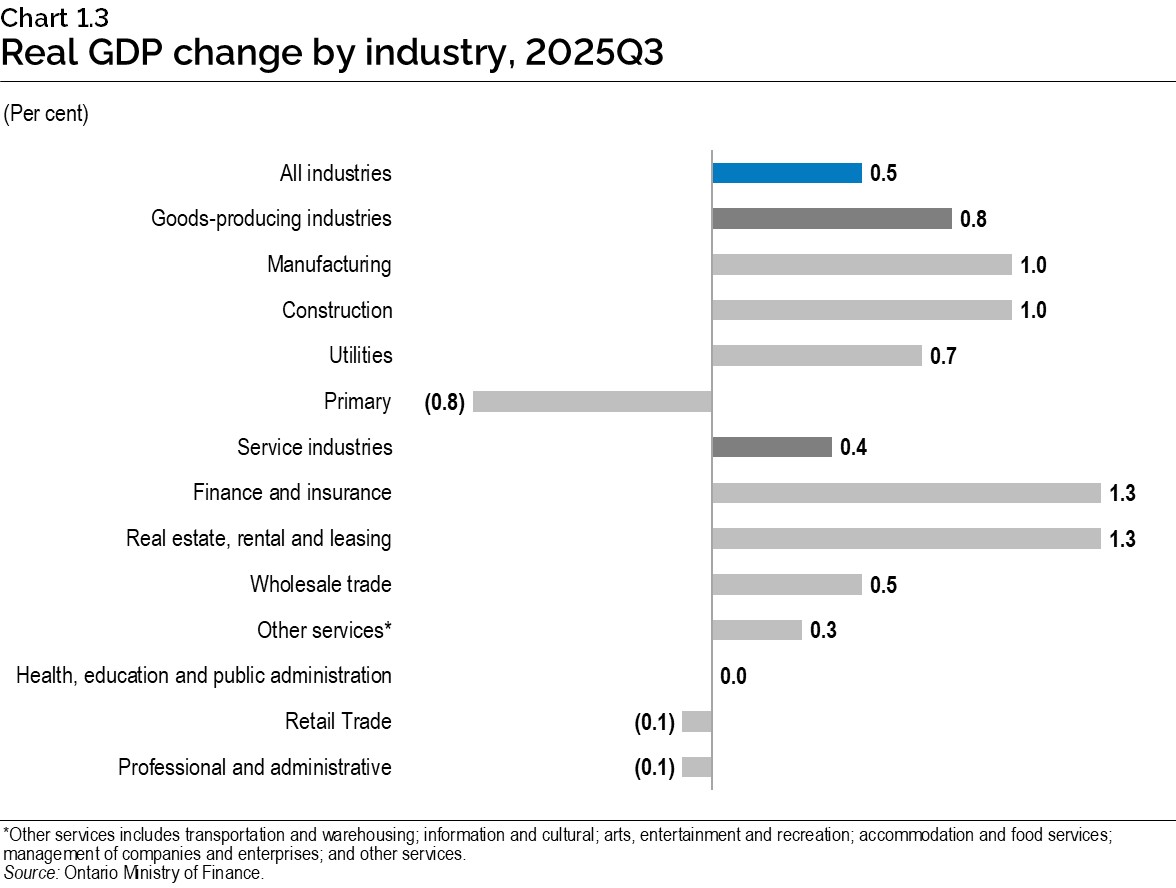
- Economic production, measured on an industry basis, increased 0.5% in the third quarter, as both goods sector output (+0.8%) and service sector production (+0.4%) rose.
| Component | 2023 | 2024 | 2024 Q4 | 2025 Q1 | 2025 Q2 | 2025 Q3 |
|---|---|---|---|---|---|---|
| Real GDP | 2.4 | 1.6 | 1.0 | 0.5 | (0.7) | 0.5 |
| Nominal GDP | 6.9 | 5.1 | 1.6 | 1.2 | (0.2) | 1.4 |
Sources: Statistics Canada and Ontario Ministry of Finance.
Expenditure details
Ontario’s real GDP rose 0.5% in the third quarter of 2025, following a 0.7% decline in the second quarter.
Household consumption spending edged down 0.1%, as lower consumption of durables (-1.4%) and non-durables (-0.6%) was partly offset by increases in consumption of semi-durables (+1.0%) and services (+0.3%).
Total business investment increased 0.8%, led by a 3.7% increase in residential investment. Non-residential investment also rose (+0.1%), while investment in machinery and equipment (-4.4%) and intellectual property products (-0.4%) declined.
Spending at all three levels of government combined edged up 0.1% in the third quarter, after increasing 1.2% in the previous quarter.
Exports (+0.2%) increased, while imports (-1.2%) declined in the third quarter. International exports (+0.1%) increased, while international imports (-1.6%) were lower. Interprovincial exports (+0.3%) and interprovincial imports (+0.2%) increased in the quarter.
Businesses accumulated inventories of $9.0 billion in the third quarter, following an accumulation of $13.8 billion in the previous quarter.
| Component | 2023 | 2024 | 2024 Q4 | 2025 Q1 | 2025 Q2 | 2025 Q3 |
|---|---|---|---|---|---|---|
| Real GDP | 2.4 | 1.6 | 1.0 | 0.5 | (0.7) | 0.5 |
| Household consumption | 2.0 | 2.2 | 1.1 | 0.5 | 0.7 | (0.1) |
| Business investment | (1.1) | (1.2) | 1.8 | 0.0 | (0.1) | 0.8 |
| Government | 1.9 | 4.5 | 0.8 | 0.0 | 1.2 | 0.1 |
| Exports | 5.1 | (0.6) | 2.0 | 0.7 | (5.1) | 0.2 |
| Imports | 1.1 | (0.3) | 0.5 | 0.6 | 0.0 | (1.2) |
| Investment in inventories ($ billions) | 3.5 | 0.8 | (10.0) | 1.3 | 13.8 | 9.0 |
Sources: Statistics Canada and Ontario Ministry of Finance.
Income details
Ontario’s nominal GDP increased 1.4% in the third quarter of 2025, after declining 0.2% in the second quarter.
Compensation of employees, which includes both wages and salaries and supplementary labour income, increased 1.3%, after edging up 0.2% in the second quarter.
Net operating surplus of corporations rose 4.0%, after declining 2.5% in the previous quarter.
Net mixed income, which is comprised of farm income, unincorporated business income and rental income, rose 2.5%, following a 1.5% increase in the previous quarter.
| Component | 2023 | 2024 | 2024 Q4 | 2025 Q1 | 2025 Q2 | 2025 Q3 |
|---|---|---|---|---|---|---|
| Nominal GDP | 6.9 | 5.1 | 1.6 | 1.2 | (0.2) | 1.4 |
| Compensation of employees | 7.2 | 6.4 | 1.4 | 0.5 | 0.2 | 1.3 |
| Net operating surplus | 2.8 | (1.1) | 5.6 | 1.1 | (2.5) | 4.0 |
| Net mixed income | 13.0 | 12.1 | 2.6 | (0.6) | 1.5 | 2.5 |
Sources: Statistics Canada and Ontario Ministry of Finance.
Price details
Economy-wide prices, as measured by the implicit price index for GDP, increased 0.9% in the third quarter, following a 0.5% increase in the second quarter.
Prices for household consumption expenditures rose 0.8%, after remaining unchanged in the second quarter.
Business investment prices declined 0.2%, following an increase of 0.2% in the previous quarter. Residential construction (-0.9%) prices were lower in the quarter. Prices for non-residential construction (+0.2%), machinery and equipment (+0.2%) and intellectual property products (+0.4%) were higher in the quarter.
Export prices (+0.6%) and import prices (+0.4%) both increased in the quarter.
| Component | 2023 | 2024 | 2024 Q4 | 2025 Q1 | 2025 Q2 | 2025 Q3 |
|---|---|---|---|---|---|---|
| GDP | 4.4 | 3.4 | 0.7 | 0.7 | 0.5 | 0.9 |
| Household consumption | 3.7 | 2.4 | 0.6 | 0.4 | 0.0 | 0.8 |
| Business investment | 4.5 | 3.3 | 0.9 | (0.5) | 0.2 | (0.2) |
| Exports | 4.2 | 3.5 | 1.5 | 2.7 | (0.8) | 0.6 |
| Imports | 1.5 | 2.7 | 1.0 | 2.7 | (1.7) | 0.4 |
Sources: Statistics Canada and Ontario Ministry of Finance.
Industry details
Ontario real GDP, measured as value-added by industry, increased 0.5% in the third quarter of 2025. Goods sector output advanced 0.8% in the quarter, while output in the service sector increased 0.4%.
Manufacturing output rose 1.0% in the third quarter, following a decline of 2.9% in the previous quarter.
Construction output increased 1.0% in the quarter, driven by an increase in both residential (+0.6%) and non-residential structures and engineering construction (+0.4%).
Primary industry output declined 0.8%, due to a decline in mining production (-2.6%). Agricultural production advanced 0.6% in the third quarter.
Utilities output increased 0.7%, following a 3.9% decrease in the previous quarter.
Service industry output rose 0.4% in the quarter, led by gains in finance and insurance (+1.3) and real estate, rental and leasing (+1.3%). Wholesale trade output advanced 0.5%, while retail trade declined 0.1% in the quarter.
| Component | 2023 | 2024 | 2024 Q4 | 2025 Q1 | 2025 Q2 | 2025 Q3 |
|---|---|---|---|---|---|---|
| Total output | 2.4 | 1.7 | 0.4 | 0.5 | (0.4) | 0.5 |
| Total goods producing industries | 0.1 | (2.3) | 0.4 | 0.2 | (1.9) | 0.8 |
| Primary | 1.9 | 2.9 | 0.1 | 0.0 | (0.1) | (0.8) |
| Utilities | 2.1 | 3.4 | (0.9) | 2.0 | (3.9) | 0.7 |
| Construction | (1.2) | (2.2) | 1.9 | (1.3) | (0.4) | 1.0 |
| Manufacturing | 0.2 | (4.6) | (0.2) | 1.0 | (2.9) | 1.0 |
| Total service industries | 3.1 | 2.8 | 0.3 | 0.6 | 0.0 | 0.4 |
| Wholesale trade | 1.4 | 0.8 | 1.9 | 1.1 | (1.0) | 0.5 |
| Retail trade | 1.4 | 1.2 | 1.7 | 1.0 | 0.8 | (0.1) |
| Transportation and warehousing | 8.0 | 3.5 | (0.1) | (0.5) | 0.4 | (0.3) |
| Information and culture | 5.6 | 2.8 | (2.5) | 1.8 | 0.2 | 1.6 |
| Finance and insurance | 0.8 | 5.2 | 0.5 | 1.1 | 1.0 | 1.3 |
| Real estate, rental and leasing | 1.9 | 3.5 | 1.3 | 0.1 | 0.2 | 1.3 |
| Management of companies and enterprises | (30.0) | (30.0) | (11.1) | (7.4) | (4.7) | (6.1) |
| Professional and administrative services | 4.1 | 1.9 | (0.9) | 0.2 | (0.8) | (0.1) |
| Education | 2.6 | 4.2 | (1.0) | 0.4 | (1.0) | 0.2 |
| Health care and social services | 3.6 | 3.7 | 0.5 | 0.5 | 0.4 | 0.4 |
| Arts, entertainment and recreation | 15.9 | 2.4 | 0.5 | 0.3 | 1.2 | 0.3 |
| Accommodation and food | 7.0 | 0.8 | 0.8 | 1.2 | 0.4 | (0.5) |
| Other services | 3.8 | (0.3) | (0.9) | 0.0 | (0.5) | (0.7) |
| Public administration | 2.6 | 2.7 | 0.4 | 0.8 | 0.3 | (0.4) |
Sources: Statistics Canada and Ontario Ministry of Finance.
Jurisdictional comparison
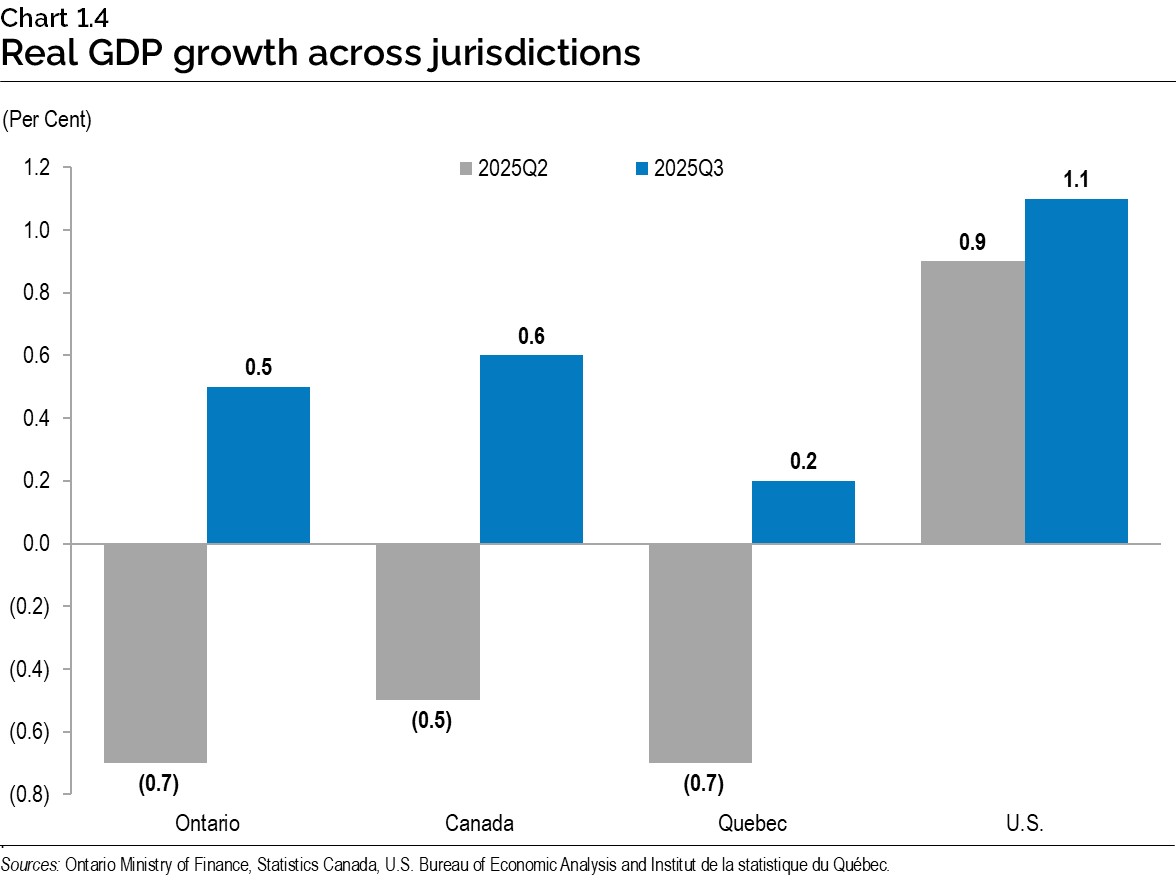
Canadian real GDP advanced 0.6% in the third quarter, following a 0.5% decline in the previous quarter. The increase in the third quarter was driven by an improved trade balance, as imports declined and exports rose modestly. The overall increase was moderated by declines in household and government spending, as well as slower accumulation of business inventories.
Quebec’s real GDP increased 0.2% in the third quarter, following a 0.7% decline in the previous quarter. The increase was primarily due to an improvement in net trade. Declines in household consumption and slower inventory accumulation moderated the overall increase.
In the U.S., real GDP advanced 1.1% in the third quarter, following a 0.9% increase in the previous quarter. The third quarter increase primarily reflected increases in consumer spending, exports, and government spending which were partially offset by a decrease in investment.
Global economic environment
Real GDP in the U.S. increased by 1.1% in the third quarter of 2025, following an increase of 0.9% in the second quarter. The third quarter increase primarily reflected increases in consumer spending, exports, and government spending which were partially offset by a decrease in investment.
Euro area real GDP grew 0.3% in the third quarter, up from 0.1% in the second quarter. Growth in the third quarter was led by gross fixed capital formation and household and government consumption expenditures. The increase was partly offset by a negative contribution from net exports.
U.K. real GDP growth increased 0.1% in the third quarter, from 0.3% in the second quarter. The third quarter gain was driven by household and government consumption, gross fixed capital formation and net exports.
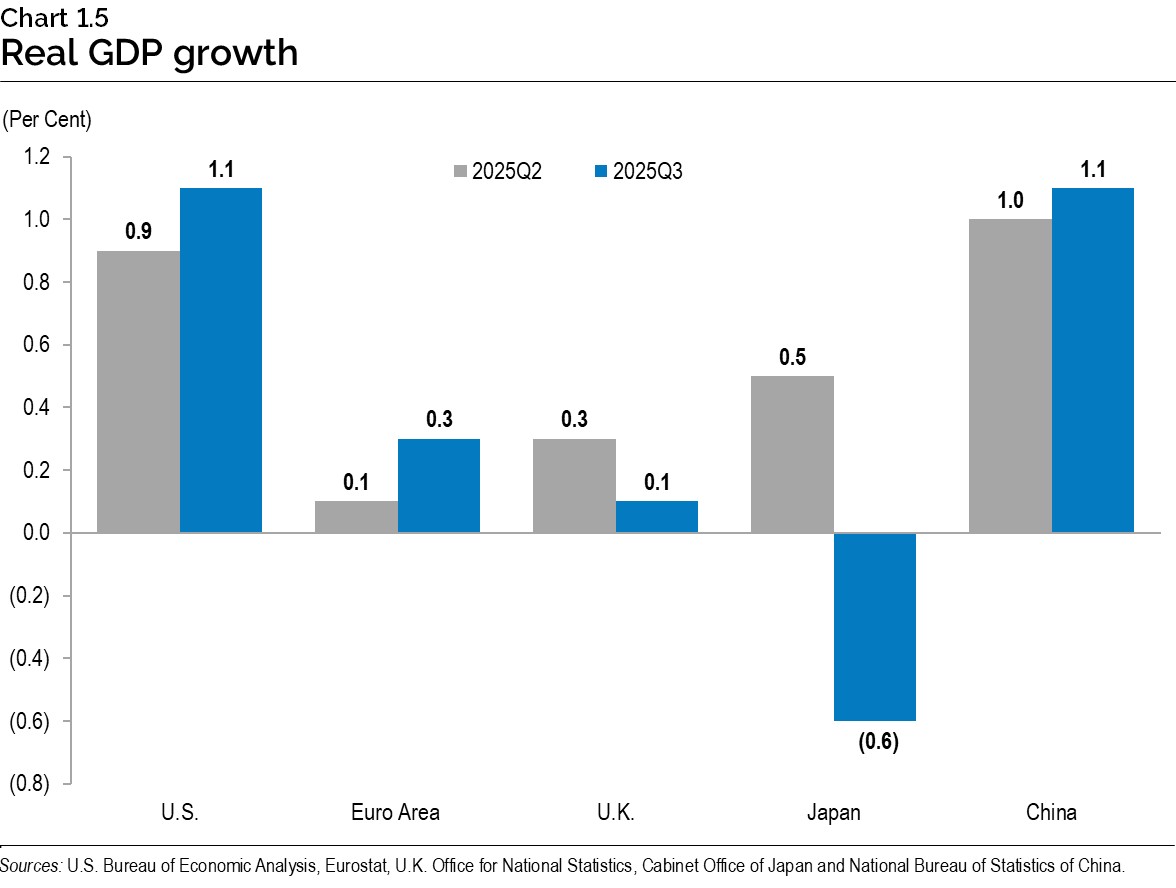
Real GDP growth in Japan declined by 0.6% in the third quarter, following a 0.5% increase in the second quarter. China’s real GDP increased by 1.1% in the third quarter, up slightly from growth of 1.0% in the second quarter.
The Bank of Canada maintained the target for the overnight rate at 2.25% at its December monetary policy meeting, following two consecutive 25-basis-point reductions in September and October. The Bank noted that Canadian real GDP growth was stronger than expected in the third quarter, reflecting trade-related volatility while final domestic demand was flat.
The U.S. Federal Reserve reduced the target range for the federal funds rate by 25 basis points to 3.50-3.75% at its December meeting, marking the third consecutive reduction since September. The Federal Reserve indicated that economic activity continues to expand at a moderate pace. Inflation has moved up and remains above the 2% target, while downside risks to employment have risen in recent months.
The yield on short-term Canadian government bonds eased in the fourth quarter of 2025. The Government of Canada three-month treasury bill yield averaged 2.2% in the fourth quarter, down from 2.6% in the third quarter. The Government of Canada 10-year bond yield declined to 3.2% in the fourth quarter from 3.4% in the third quarter.
After weakening in the second and third quarters of 2025, the U.S. dollar stabilized in the fourth quarter, posting a modest gain against other major currencies. The Canadian dollar averaged 71.7 cents US in the fourth quarter, down from 72.6 cents US in the third quarter.
Oil prices declined amid global oversupply and soft demand conditions. The West Texas Intermediate (WTI) crude oil price averaged US$60 per barrel in the fourth quarter, down from US$66 per barrel in the third quarter.
| Component | 2024 | 2025 | 2024 Q4 | 2025 Q1 | 2025 Q2 | 2025 Q3 | 2025 Q4 |
|---|---|---|---|---|---|---|---|
| U.S. real GDP growth (per cent) | 2.8 | – | 0.5 | (0.2) | 0.9 | 1.1 | – |
| West Texas Intermediate (WTI) crude oil (US$ per barrel) | 77 | 65 | 71 | 72 | 65 | 66 | 60 |
| Canadian dollar (cents US) | 73.0 | 71.6 | 71.5 | 69.7 | 72.3 | 72.6 | 71.7 |
| Three-month treasury bill rate1 (per cent) | 4.4 | 2.6 | 3.5 | 2.9 | 2.6 | 2.6 | 2.2 |
| 10-year government bond rate (per cent) | 3.3 | 3.2 | 3.2 | 3.1 | 3.2 | 3.4 | 3.2 |
[1] Government of Canada interest rates.
Sources: U.S. Bureau of Economic Analysis; U.S. Energy Information Administration, and Bank of Canada.
Appendix A: OEA release dates
The Fiscal Sustainability, Transparency and Accountability Act, 2019 states that the quarterly Ontario Economic Accounts should be released within 45 days of the Statistics Canada release of the National Income and Expenditure Accounts.
In compliance with the legislation, the OEA will be released according to the following schedule:
| Reference Period | Expected Statistics Canada release of National Income and Expenditure Accounts | Corresponding deadline for the release of Ontario Economic Accounts |
|---|---|---|
| Fourth quarter (October-December) 2025 | February 27, 2026 | By April 13, 2026 |
| First quarter (January-March) 2026 | May 29, 2026 | By July 13, 2026 |
| Second quarter (April-June) 2026 | August 28, 2026 | By October 13, 2026 |
| Third quarter (July-September) 2026 | November 30, 2026 | By January 14, 2027 |
| Fourth quarter (October-December) 2026 | March 1, 2027 | By April 15, 2027 |
Appendix B: Structure of the Ontario economy
Appendix C: How GDP is measured
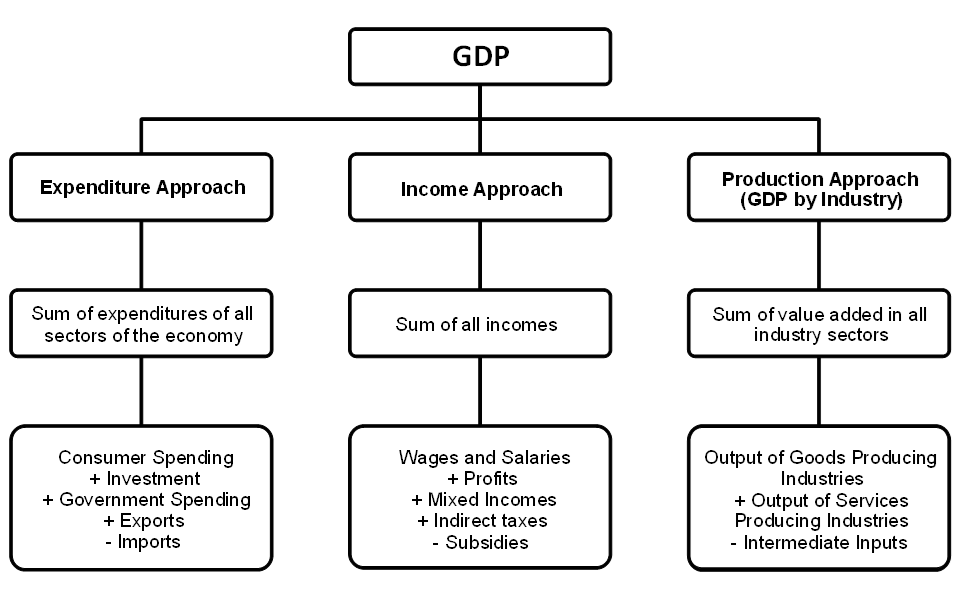
The Ontario Economic Accounts provide measurements of GDP using three different methodologies, by expenditure, income and industry.
The GDP by expenditure approach defines GDP as the aggregate of all expenditures on final consumption, gross capital formation and net trade by consumers, governments and businesses that occur within Ontario’s economy over a given time period. This measurement of GDP can also be defined as the sum of consumer spending, gross investment, government spending and net trade.
The GDP by income approach equates GDP to the total income earned through contributions to production within Ontario’s economy by labour and capital over a given time period. That is, GDP is the sum of all wages and salaries paid to employees, the gross operating surplus of businesses, gross mixed income and indirect taxes less subsidies.
The GDP by industry approach measures GDP by calculating the total output of the goods and services producing industries within Ontario’s economy and subtracting the cost of intermediate inputs used in final production. This approach can also be referred to as the value-added approach as it quantifies the additional value generated by industries through the production of final products within the economy.
For a full list of definitions used in the Ontario Economic Accounts, please see Statistics Canada’s System of Macroeconomic Accounts Glossary at https://www150.statcan.gc.ca/n1/pub/13-605-x/gloss/gloss-a-eng.htm.
Accessible chart descriptions
Chart 1.1: Real GDP growth
The bar chart illustrates Ontario’s quarterly per cent real GDP growth from the first quarter of 2022 to the third quarter of 2025. In the four quarters of 2022, real GDP growth was 1.0%, 1.2%, 0.4% and -0.2%, respectively. In the four quarters of 2023, real GDP growth was 1.3%, 0.6%, 0.4% and 0.2%, respectively. In the four quarters of 2024, real GDP growth was 0.4%, 0.4%, 0.3% and 1.0%, respectively. In 2025, real GDP increased 0.5% in the first quarter, declined 0.7% in the second quarter and increased 0.5% in the third quarter.
Source: Ontario Ministry of Finance.
Chart 1.2: Nominal GDP growth
The bar chart illustrates Ontario’s quarterly per cent nominal GDP growth from the first quarter of 2022 to the third quarter of 2025. In the four quarters of 2022, GDP growth was 2.7%, 4.0%, 0.6% and 0.7%, respectively. In the four quarters of 2023, GDP growth was 1.6%, 2.6%, 1.9% and 1.7%, respectively. In the four quarters of 2024, GDP growth was 0.2%, 1.5%, 1.0% and 1.6%, respectively. In 2025, nominal GDP rose 1.2% in the first quarter, declined 0.2% in the second quarter and increased 1.4% in the third quarter.
Source: Ontario Ministry of Finance.
Chart 1.3: Real GDP Change by Industry, 2025 Q3
The horizontal bar chart illustrates the per cent change in real GDP by industry for the third quarter of 2025. The output of all industries increased 0.5% in the quarter. Output increased in goods-producing industries (+0.8%), with industry changes as follows: manufacturing (+1.0%); construction (+1.0%); utilities (+0.7%); and primary (−0.8%). Output in the service industries increased 0.4%, including industry changes as follows: finance and insurance (+1.3%); real estate, rental and leasing (+1.3%); wholesale trade (+0.5%); other services* (+0.3%); health, education and public administration (0.0%); retail trade (-0.1%); and professional and administrative services (−0.1%).
*Other services include transportation and warehousing; information and cultural; arts, entertainment, and recreation; accommodation and food services; management of companies and enterprises; and other services.
Source: Ontario Ministry of Finance.
Chart 1.4: Real GDP growth across jurisdictions
This bar chart shows quarterly percentage changes in real GDP for Ontario, Canada, Quebec and the U.S. for the second quarter of 2025 and third quarter of 2025. Ontario real GDP decreased 0.7% in the second quarter and increased 0.5% in the third quarter. Canadian real GDP decreased 0.5% in the second quarter and increased 0.6% in the third quarter. Quebec real GDP declined 0.7% in the second quarter and increased 0.2% in the third quarter. U.S. real GDP increased 0.9% in the second quarter and increased 1.1% in the third quarter.
Sources: Ontario Ministry of Finance, Statistics Canada, U.S. Bureau of Economic Analysis and Institut de la statistique du Québec.
Chart 1.5: Real GDP growth
This bar chart shows quarterly percentage changes in real GDP for the U.S., the euro area, the United Kingdom, Japan and China, for the second quarter of 2025 and third quarter of 2025. U.S. real GDP increased 0.9% in the second quarter and increased 1.1% in the third quarter. Euro area real GDP increased 0.1% in the second quarter and 0.3% in the third quarter. Real GDP in the United Kingdom increased 0.3% in the second quarter and 0.1% in the third quarter. Japan’s real GDP increased 0.5% in the second quarter and declined 0.6% in the third quarter. China’s real GDP increased 1.0% in the second quarter and 1.1% in the third quarter.
Sources: U.S. Bureau of Economic Analysis, Eurostat, U.K. Office for National Statistics, Cabinet Office of Japan, and National Bureau of Statistics of China.
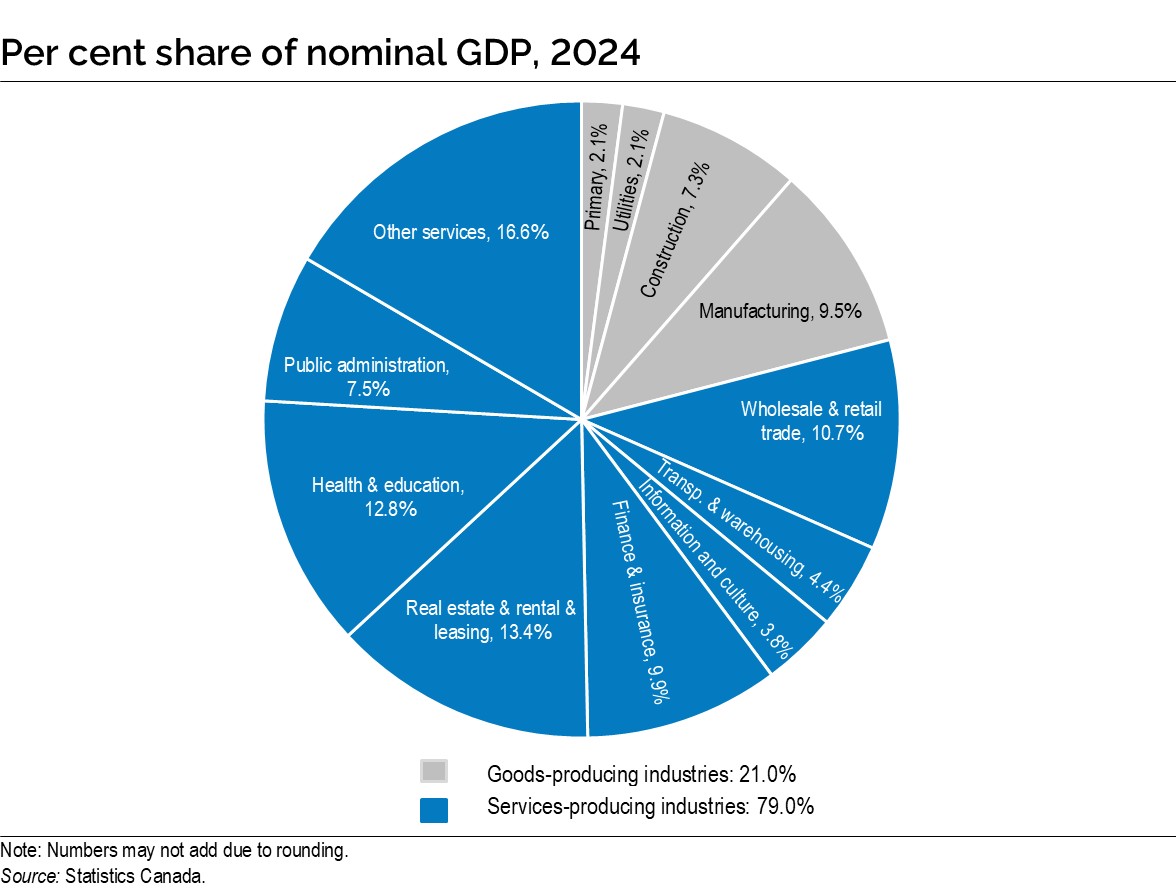
Chart: Appendix B, Per Cent Share of Nominal GDP, 2024
This pie chart shows the percent share of nominal GDP by industry for 2024. Goods-producing industries accounted for 21.0% of Ontario’s nominal GDP with industry shares as follows: manufacturing (9.5%); construction (7.3%); utilities (2.1%) and primary industries (2.1%). Services-producing industries accounted for 79.0% of Ontario’s nominal GDP with industry shares as follows: wholesale and retail trade (10.7%); transportation and warehousing (4.4%); information and culture (3.8%); finance and insurance (9.9%); real estate, rental and leasing (13.4%); health and education (12.8%); public administration (7.5%); and other services (16.6%).
Note: Numbers may not add due to rounding.
Source: Statistics Canada.
Chart : Appendix C, GDP measurement methods
- Expenditure Approach
- Sum of expenditures of all sectors of the economy
- Consumer Spending + Investment + Government Spending + Exports – Imports
- Income Approach
- Sum of all incomes
- Wage and Salaries + Profits + Mixed Incomes + Indirect taxes – Subsidies
- Production Approach (GDP by Industry)
- Sum of value added in all industry sectors
- Output of Goods Producing Industries + Output of Services Producing Industries – Intermediate Inputs